算法题

将数字转换成千分位表示【微信】

将数字 87463297 转成 87，463，297

解法一:

function toThree(value) {
  let list = String(value).split("").reverse();
  let temp = [];
  for (let i = 0, len = list.length; i < len; i = i + 3) {
    temp.push(list.slice(i, i + 3).join(""));
  }
  return temp.join(",").split("").reverse().join("");
}

console.log(toThree(87463297));

解法二：使用正则表达式

利用正则的零宽度正预测先行断言(?=exp)，名字有点难记，意思是它断言自身出现的位置的后面能匹配表达式 exp，对此概念还不明白的可以戳这里 (opens new window)

function toThree(value) {
  const val = String(value);
  return val.replace(/(\d{1,3})(?=(\d{3})+)/g, function (el) {
    return el + ",";
  });
}

console.log(toThree(87463297));

二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]] 示例 2：

输入：root = [1] 输出：[[1]] 示例 3：

输入：root = [] 输出：[]

var levelOrder = function (root) {
  //二叉树的层序遍历
  let res = [],
    queue = [];
  queue.push(root);
  if (root === null) {
    return res;
  }
  while (queue.length !== 0) {
    // 记录当前层级节点数
    let length = queue.length;
    //存放每一层的节点
    let curLevel = [];
    for (let i = 0; i < length; i++) {
      let node = queue.shift();
      curLevel.push(node.val);
      // 存放当前层下一层的节点
      node.left && queue.push(node.left);
      node.right && queue.push(node.right);
    }
    //把每一层的结果放到结果数组
    res.push(curLevel);
  }
  return res;
};

判断二叉树是否为平衡二叉树

定义:一棵空树或它的任意节点的左右两个子树的高度差的绝对值均不超过 1。

解答一:自顶向下（暴力法）

根据二叉树的定义，我们可以递归遍历二叉树的每一个节点来，求出每个节点的左右子树的高度，如果每个节点的左右子树的高度相差不超过 1，按照定义，它就是一颗平衡二叉树。

function isBalanced(root) {
  if (!root) return true;
  return (
    Math.abs(depth(root.left) - depth(root.right)) <= 1 &&
    isBalanced(root.left) &&
    isBalanced(root.right)
  );
}
function depth(node) {
  if (!node) return -1;
  return 1 + Math.max(depth(node.left), depth(node.right));
}

function TreeNode(name, left, right) {
  this.name = name;
  this.left = left;
  this.right = right;
}

let bNode = new TreeNode("b", null, null);
let dNode = new TreeNode("d", null, null);
let eNode = new TreeNode("e", null, null);
let cNode = new TreeNode("c", dNode, eNode);
let aNode = new TreeNode("a", bNode, cNode);

console.log(isBalanced(aNode));

// a -> b
// a -> c -> d
// a -> c -> e

复杂度分析:

• 时间复杂度:O(n²)，计算 depth 存在大量冗余操作
• 空间复杂度:O(n)

解答二:自底向上（优化）

解题思路: 利用后续遍历二叉树（左右根），从底至顶返回子树最大高度，判定每个子树是不是平衡树 ，如果平衡，则使用它们的高度判断父节点是否平衡，并计算父节点的高度，如果不平衡，返回 -1 。

遍历比较二叉树每个节点 的左右子树深度:

• 比较左右子树的深度，若差值大于 1 则返回一个标记 -1 ，表示当前子树不平衡
• 左右子树有一个不是平衡的，或左右子树差值大于 1 ，则二叉树不平衡
• 若左右子树平衡，返回当前树的深度（左右子树的深度最大值 +1 ）

let isBalanced = function (root) {
  return balanced(root) !== -1;
};
let balanced = function (node) {
  if (!node) return 0;
  const left = balanced(node.left);
  const right = balanced(node.right);
  if (left === -1 || right === -1 || Math.abs(left - right) > 1) {
    return -1;
  }
  return Math.max(left, right) + 1;
};
function TreeNode(name, left, right) {
  this.name = name;
  this.left = left;
  this.right = right;
}

let bNode = new TreeNode("b", null, null);
let dNode = new TreeNode("d", null, null);
let eNode = new TreeNode("e", null, null);
let cNode = new TreeNode("c", dNode, eNode);
let aNode = new TreeNode("a", bNode, cNode);

console.log(isBalanced(aNode));

• 时间复杂度: O ( n )，其中 n 是二叉树中的节点个数。使用自底向上的递归，每个节点的计算高度和判断是否平衡都只需要处理一次，最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 O ( n ) 。

• 空间复杂度: O ( n ) ，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

判断二叉树是否为对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树  [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个  [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

let isSymmetric = function (root) {
  const check = (left, right) => {
    if (left == null && right == null) {
      return true;
    }
    if (left && right) {
      return (
        left.val === right.val &&
        check(left.left, right.right) &&
        check(left.right, right.left)
      );
    }
    return false; // 一个子树存在一个不存在，肯定不对称
  };
  if (root == null) {
    // 如果传入的root就是null，对称
    return true;
  }
  return check(root.left, root.right);
};

如何判断是否为子树

此题来自leetcode (opens new window)

输入两棵二叉树 A 和 B，判断 B 是不是 A 的子结构。(约定空树不是任意一个树的子结构)

B 是 A 的子结构， 即 A 中有出现和 B 相同的结构和节点值。

例如: 给定的树 A:

     3
    / \
   4   5
  / \
 1   2

给定的树 B:

   4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1:

输入:A = [1,2,3], B = [3,1] 输出:false 示例 2:

输入:A = [3,4,5,1,2], B = [4,1] 输出:true

function isSubStructure(A, B) {
  if (!B || !A) return false;
  return find(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}

function find(A, B) {
  if (!B) return true;
  if (!A || A.val != B.val) return false;
  return find(A.left, B.left) && find(A.right, B.right);
}

二叉树的最大深度

var maxDepth = function (root) {
  return dfs(root);
};

const dfs = (root) => {
  if (!root) return 0;
  return Math.max(dfs(root.left), dfs(root.right)) + 1;
};

二叉树某个子树之和是否为某个数字

给你二叉树的根节点  root 和一个表示目标和的整数  targetSum ，判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和  targetSum 。

叶子节点 是指没有子节点的节点。

示例 1:

**输入:**root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 **输出:**true

示例 2:

输入: root = [1,2,3], targetSum = 5 输出: false

**示例 3: **

输入: root = [1,2], targetSum = 0 输出: false

let hasPathSum = function (root, targetSum) {
  // 深度优先遍历
  if (root === null) {
    //1.刚开始遍历时
    //2.递归中间 说明该节点不是叶子节点
    return false;
  }
  if (root.left === null && root.right === null) {
    return root.val - targetSum === 0;
  }
  // 拆分成两个子树
  return (
    hasPathSum(root.left, targetSum - root.val) ||
    hasPathSum(root.right, targetSum - root.val)
  );
};

求数组里面最大连续项的和( 连续子数组的最大和)

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。

示例 1:

输入: nums = [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释:  连续子数组  [4,-1,2,1] 的和最大，为  6。

let maxSubArray = function (nums) {
  let pre = 0,
    maxAns = nums[0];
  nums.forEach((x) => {
    pre = Math.max(pre + x, x);
    maxAns = Math.max(maxAns, pre);
  });
  return maxAns;
};

const nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4];
console.log(maxSubArray(nums));

求一个数组最大子项的和，要求这些子项在数组中的位置不是连续的(打家劫舍)

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1:

输入:[1,2,3,1] **输出:**4 **解释:**偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。   偷窃到的最高金额 = 1 + 3 = 4 。

示例 2:

输入:[2,7,9,3,1] **输出:**12 **解释:**偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。   偷窃到的最高金额 = 2 + 9 + 1 = 12 。

解题思路

方法一，动态规划:

1. 定义 dp[i] 表示考虑抢劫 nums[0...i] 所能获得的最大收益(注意这里是闭区间)
2. 由于不可以同时偷相邻的房屋，所以在当前位置为 i 房屋可盗窃的最大值要么就是 i-1 房屋可盗窃的最大值，要么就是 i-2 房屋可盗窃的最大值加上当前房屋的值，二者之间取最大值
3. 所以状态转移方程为:dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])
4. 时间复杂度为 O(n)

代码参考自这里 (opens new window)

/**
 * @param {number[]} nums
 * @return {number}
 * 动态规划
 * dp[i] 表示考虑抢劫 nums[0...i] 所能获得的最大收益
 * dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])
 */
let rob = function (nums) {
  let n = nums.length;
  if (n === 0) {
    // 如果是空数组直接返回0
    return 0;
  }
  let dp = new Array(n).fill(-1);
  dp[0] = nums[0]; // 初始化 dp[0]
  dp[1] = Math.max(nums[0], nums[1]); // 初始化 dp[1]
  // 遍历推导至需要求解的 dp[n-1]
  for (let i = 2; i < n; i++) {
    dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
  }
  return dp[n - 1];
};

字符串找最长的不重复子串

题目描述: 请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

示例  1:

输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是  "wke"，所以其长度为 3。   请注意，你的答案必须是 子串 的长度，"pwke"  是一个子序列，不是子串。

解题思路

1. 使用滑动窗口算法；
2. 当遇到重复字符的时候删除重复字符前面（包括这个重复字符）的所有字符；
3. 记录达到不重复的最长子字符长度；
4. 循坏之后有更长的不重复子串就更新我们的不重复最大子字符串长度；

代码

let lengthOfLongestSubstring = function (s) {
  let str = [],
    maxlength = 0;
  for (let i = 0; i < s.length; i++) {
    let index = str.indexOf(s[i]);
    if (index != -1) {
      str.splice(0, index + 1);
    }
    str.push(s[i]);
    maxlength = Math.max(maxlength, str.length);
  }
  return maxlength;
};

请求并发限制

我们知道，promise 并不是因为调用 Promise.all 才执行，而是在实例化 promise 对象的时候就执行了，在理解这一点的基础上，要实现并发限制，只能从 promise 实例化上下手。

// es7
async function asyncPool(poolLimit, array, iteratorFn) {
  const ret = [];
  const executing = [];
  for (const item of array) {
    const p = Promise.resolve().then(() => iteratorFn(item, array));
    ret.push(p);

    if (poolLimit <= array.length) {
      // promise执行完毕，从executing数组中删除
      const e = p.then(() => executing.splice(executing.indexOf(e), 1));
      executing.push(e);
      if (executing.length >= poolLimit) {
        // 使用竞速策略，当有一个promise执行完毕，继续初始化promise并放入executing中
        await Promise.race(executing);
      }
    }
  }
  return Promise.all(ret);
}

// 测试用例
let count = 0;
const timeout = (curItem) => {
  return new Promise((resolve) => {
    count++;
    setTimeout(() => {
      console.log(curItem, "当前并发量:", count--);
      resolve();
    }, Math.random() * 5000);
  });
};
return asyncPool(2, [1000, 5000, 3000, 2000], timeout).then((results) => {
  console.log(results);
});

函数柯里化实现

本章参考: 函数柯里化实现 (opens new window)

什么是函数柯里化? 只传递给函数一部分参数来调用它，让它返回一个函数去处理剩下的参数。用公式表示就是我们要做的事情其实是

fn(a,b,c,d)=>fn(a)(b)(c)(d)；

fn(a,b,c,d)=>fn(a，b)(c)(d)；

fn(a,b,c,d)=>fn(a)(b，c，d)；

......

再或者这样:

fn(a,b,c,d)=>fn(a)(b)(c)(d)()；

fn(a,b,c,d)=>fn(a)；fn(b)；fn(c)；fn(d)；fn()；

但不是这样:(下面为偏函数)

fn(a,b,c,d)=>fn(a)；

fn(a,b,c,d)=>fn(a，b)；

const curry = (fn, ...arg) => {
  let all = arg || [],
    length = fn.length;
  return (...rest) => {
    let _args = all.slice(0); //拷贝新的all，避免改动公有的all属性，导致多次调用_args.length出错
    _args.push(...rest);
    if (_args.length < length) {
      //在没有达到fn参数个数时，返回当前fn函数引用
      return curry.call(this, fn, ..._args);
    } else {
      //当达到了fn的参数，那么就调用fn函数
      return fn.apply(this, _args);
    }
  };
};

//测试

let test = curry(function (a, b, c) {
  console.log(a + b + c);
});
test(1, 2, 3);
test(1, 2)(3);
test(1)(2)(3);

树状图寻找

我有一个 from to 的树状图结构，请使用JS编写一段算法要求 找出 start 和 end 的多条路径

let graph = [{
    from: 'A',
    to: 'B'
  },
  {
    from: 'A',
    to: 'C'
  },
  {
    from: 'B',
    to: 'D'
  },
  {
    from: 'B',
    to: 'E'
  },
  {
    from: 'C',
    to: 'F'
  },
  {
    from: 'E',
    to: 'F'
  }
];

function findPaths(graph, start, end) {
  let paths = [];
  let visited = new Set();
  
  function dfs(node, path) {
    visited.add(node);
    path.push(node);
    
    if (node === end) {
      paths.push([...path]);
    } else {
      let neighbors = graph.filter(edge => edge.from === node).map(edge => edge.to);
      
      for (let nextNode of neighbors) {
        if (!visited.has(nextNode)) {
          dfs(nextNode, path);
        }
      }
    }
    
    path.pop(); // 回溯，将当前节点从路径中删除
    visited.delete(node); // 取消标记当前节点
  }
  
  dfs(start, []);
  
  return paths;
}

console.log(findPaths(graph, 'A', 'F'));

实现一个异步求和函数

// 提供一个asyncAdd法如下，需要实现一个await sum(...args)函数;

function asyncAdd(a, b, callback) {
  setTimeout(function () {
    callback(null, a + b);
  }, 1000);
}

// 自己写的代码
function createAdd(a, b = 0) {
  return new Promise((resolve) => {
    asyncAdd(a, b, (err, result) => {
      if (!err) {
        resolve(result);
      }
    });
  });
}

async function sum(...args) {
  if (args.length > 1) {
    const result = [];
    for (let i = 0; i < args.length; i = i + 2) {
      result.push(createAdd(args[i], args[i + 1]));
    }
    return sum(...(await Promise.all(result)));
  }
  return args[0];
}

// 测试用例
sum(1, 2, 3).then((res) => {
  console.log(res);
});

实现函数的防抖和节流函数

所谓防抖，就是指触发事件后在 n 秒内函数只能执行一次，如果在 n 秒内又触发了事件，则会重新计算函数执行时间。

function debounce(func, wait) {
  let timeout;
  return function () {
    let context = this;
    let args = arguments;
    if (timeout) clearTimeout(timeout);
    timeout = setTimeout(() => {
      func.apply(context, args);
    }, wait);
  };
}

所谓节流，就是指连续触发事件但是在 n 秒中只执行一次函数

function throttle(func, wait) {
  let timeout;
  return function () {
    let context = this;
    let args = arguments;
    if (!timeout) {
      timeout = setTimeout(() => {
        timeout = null;
        func.apply(context, args);
      }, wait);
    }
  };
}

最长回文字符串

暴力破解

/**
 * 整体思路:
 * 外面的两层循环找到所有子串，然后判断对应的子串是否为回文字符串。
 * @param {*} s
 */
function longestPalindrome(s) {
  let length = s.length;
  let result = "";
  for (let i = 0; i < length; i++) {
    for (let j = i + 1; j <= length; j++) {
      let str = s.slice(i, j);
      let f = str.split("").reverse().join("");

      if (str == f) {
        result = str.length > result.length ? str : result;
      }
    }
  }
  return result;
}

//测试
console.log("====================================");
console.log(longestPalindrome("babccabcbacaacb")); //cabcbac
console.log("====================================");

判断链表是否为回文链表

请判断一个链表是否为回文链表。

示例 1:

输入: 1->2 输出: false 示例 2:

输入: 1->2->2->1 输出: true

const isPalindrome = (head) => {
  const vals = [];
  while (head) {
    // 丢进数组里
    vals.push(head.val);
    head = head.next;
  }
  let start = 0,
    end = vals.length - 1; // 双指针
  while (start < end) {
    if (vals[start] != vals[end]) {
      // 理应相同，如果不同，不是回文
      return false;
    }
    start++;
    end--; // 双指针移动
  }
  return true; // 循环结束也没有返回false，说明是回文
};

大数相乘【微信】

function multiplyBigNum(num1, num2) {
  //判断输入是不是数字
  if (isNaN(num1) || isNaN(num2)) return "";
  let len1 = num1.length,
    len2 = num2.length;
  let pos = [];

  //j放外面，先固定被乘数的一位，分别去乘乘数的每一位，更符合竖式演算法
  for (let j = len2 - 1; j >= 0; j--) {
    for (let i = len1 - 1; i >= 0; i--) {
      //两个个位数相乘，最多产生两位数，index1代表十位，index2代表个位
      let index1 = i + j,
        index2 = i + j + 1;
      //两个个位数乘积加上当前位置个位已累积的数字，会产生进位，比如08 + 7 = 15，产生了进位1
      let mul = num1[i] * num2[j] + (pos[index2] || 0);
      //mul包含新计算的十位，加上原有的十位就是最新的十位
      pos[index1] = Math.floor(mul / 10) + (pos[index1] || 0);
      //mul的个位就是最新的个位
      pos[index2] = mul % 10;
    }
  }

  //去掉前置0
  let result = pos.join("").replace(/^0+/, "");

  return result || "0";
}

大数相加（完整版本）

请使用 js 实现一个简单的大数相加函数 sum，要求实现正数相加及正负数相加。

测试函数:

console.log(sum("9007199254740991", "1229007199254740993443"));
console.log(sum("9007199254740991", "-1229007199254740993443"));

/**
 * 大数相加
 * @param {*} a
 * @param {*} b
 */
function addSame(num1, num2) {
  let isAddOne = false; //是否加一
  let nums = "";
  let len = Math.max(num1.length, num2.length);
  num1.length < num2.length
    ? (num1 = num1.padStart(len, "0"))
    : (num2 = num2.padStart(len, "0"));
  for (let i = len - 1; i >= 0; i--) {
    let temp = 0;
    temp = parseInt(num1[i]) + parseInt(num2[i]);
    isAddOne && temp++;
    isAddOne = temp >= 10;
    nums = (isAddOne ? temp - 10 : temp) + nums + "";
  }
  isAddOne && (nums = 1 + nums);
  return nums;
}

/**
 * 大数相减，保证第一个数字大于第二个数字
 * @param {*} num1
 * @param {*} num2
 */
function sub(num1, num2) {
  if (num1 === num2) return "0";
  let len = Math.max(num1.length, num2.length);
  num1 = num1.padStart(len, 0);
  num2 = num2.padStart(len, 0);

  let flag = 0,
    result = "",
    temp;
  for (let i = len - 1; i >= 0; i--) {
    temp = parseInt(num1[i]) - flag - parseInt(num2[i]);
    if (temp < 0) {
      result = 10 + temp + result;
      flag = 1;
    } else {
      result = temp + result;
      flag = 0;
    }
  }
  result = result.replace(/^0+/, "");
  return result;
}
/**
 * 判断两个数字谁比较大，要考虑正负情况
 * @param {*} a
 * @param {*} b
 */
function isRight(a, b) {
  // 运算结果应该为正数吗
  const one = a.replace(/-?0*/, "");
  const two = b.replace(/-?0*/, "");
  let isBBig = false;
  if (two.length > one.length) {
    isBBig = true;
  } else if (two.length === one.length) {
    const oneList = one.split("");
    const twoList = two.split("");
    for (let index = 0; index < oneList.length; index++) {
      if (twoList[index] > oneList[index]) {
        isBBig = true;
        break;
      }
    }
  }

  return isBBig;
}

function sum(a, b) {
  if (a.indexOf("-") === 0 && b.indexOf("-") === 0) {
    return "-" + addSame(a, b);
  } else if (a.indexOf("-") === -1 && b.indexOf("-") === -1) {
    return addSame(a, b);
  } else {
    let isBBig = isRight(a, b); // 此处的大小是按照绝对值的
    let resultIsRight = false; //结果为正数？
    const absA = a.replace(/-?0*/, "");
    const absB = b.replace(/-?0*/, "");

    if (a.indexOf("-") !== -1) {
      // a大
      resultIsRight = isBBig ? true : false; // a为负数，b为正数，但是b绝对值大，所以结果为正数
    } else {
      resultIsRight = isBBig ? false : true; // a为正数，b为负数，但是b绝对值大，所以结果为负数
    }
    // 获取谁比较大，需要考虑-00001243这种情况，不能完全使用字符串长度进行比较
    return (
      (resultIsRight ? "" : "-") +
      sub(isBBig ? absB : absA, isBBig ? absA : absB)
    ); // 保证第一个数字比较大，第二个数字比较小，变成大数相减了
  }
}

console.log(sum("9007199254740991", "1229007199254740993443")); // 1229016206453995734434
console.log(sum("9007199254740991", "-1229007199254740993443")); // -1228998192055486252452

异步代码顺序执行

题目:要求实现 createFlow 函数，支持 flow 嵌套且串行执行

const delay = (ms) => new Promise((resolve) => setTimeout(resolve, ms));

const subFlow = createFlow([() => delay(1000).then(() => log("c"))]);
const log = console.log;
createFlow([
  () => log("a"),
  () => log("b"),
  subFlow,
  [() => delay(1000).then(() => log("d")), () => log("e")],
]).run(() => {
  console.log("done");
});

// 需要按照 a,b,延迟1秒,c,延迟1秒,d,e, done 的顺序打印

代码

function createFlow(effets = []) {
  const sources = effets.slice().flat();
  return {
    async run(callback) {
      for (const effect of sources) {
        typeof effect === "function" ? await effect() : effect.run();
      }

      typeof callback === "function" && callback();
    },
  };
}

自定义实现一个简单的 Promise

// 实现一个简单 Promise A+ 规范的 Promise 库， 需支持 then(resolve, reject)和catch

try {
  module.exports = Promise;
} catch (e) {}

function Promise(executor) {
  let self = this;

  self.status = "pending";
  self.onResolvedCallback = [];
  self.onRejectedCallback = [];

  function resolve(value) {
    if (value instanceof Promise) {
      return value.then(resolve, reject);
    }
    setTimeout(function () {
      // 异步执行所有的回调函数
      if (self.status === "pending") {
        self.status = "resolved";
        self.data = value;
        for (let i = 0; i < self.onResolvedCallback.length; i++) {
          self.onResolvedCallback[i](value);
        }
      }
    });
  }

  function reject(reason) {
    setTimeout(function () {
      // 异步执行所有的回调函数
      if (self.status === "pending") {
        self.status = "rejected";
        self.data = reason;
        for (let i = 0; i < self.onRejectedCallback.length; i++) {
          self.onRejectedCallback[i](reason);
        }
      }
    });
  }

  try {
    executor(resolve, reject);
  } catch (reason) {
    reject(reason);
  }
}

function resolvePromise(promise2, x, resolve, reject) {
  let then;
  let thenCalledOrThrow = false;

  if (promise2 === x) {
    return reject(new TypeError("Chaining cycle detected for promise!"));
  }

  if (x instanceof Promise) {
    if (x.status === "pending") {
      //because x could resolved by a Promise Object
      x.then(function (v) {
        resolvePromise(promise2, v, resolve, reject);
      }, reject);
    } else {
      //but if it is resolved, it will never resolved by a Promise Object but a static value;
      x.then(resolve, reject);
    }
    return;
  }

  if (x !== null && (typeof x === "object" || typeof x === "function")) {
    try {
      then = x.then; //because x.then could be a getter
      if (typeof then === "function") {
        then.call(
          x,
          function rs(y) {
            if (thenCalledOrThrow) return;
            thenCalledOrThrow = true;
            return resolvePromise(promise2, y, resolve, reject);
          },
          function rj(r) {
            if (thenCalledOrThrow) return;
            thenCalledOrThrow = true;
            return reject(r);
          }
        );
      } else {
        resolve(x);
      }
    } catch (e) {
      if (thenCalledOrThrow) return;
      thenCalledOrThrow = true;
      return reject(e);
    }
  } else {
    resolve(x);
  }
}

Promise.prototype.then = function (onResolved, onRejected) {
  let self = this;
  let promise2;
  onResolved =
    typeof onResolved === "function"
      ? onResolved
      : function (v) {
          return v;
        };
  onRejected =
    typeof onRejected === "function"
      ? onRejected
      : function (r) {
          throw r;
        };

  if (self.status === "resolved") {
    return (promise2 = new Promise(function (resolve, reject) {
      setTimeout(function () {
        // 异步执行onResolved
        try {
          let x = onResolved(self.data);
          resolvePromise(promise2, x, resolve, reject);
        } catch (reason) {
          reject(reason);
        }
      });
    }));
  }

  if (self.status === "rejected") {
    return (promise2 = new Promise(function (resolve, reject) {
      setTimeout(function () {
        // 异步执行onRejected
        try {
          let x = onRejected(self.data);
          resolvePromise(promise2, x, resolve, reject);
        } catch (reason) {
          reject(reason);
        }
      });
    }));
  }

  if (self.status === "pending") {
    // 这里之所以没有异步执行，是因为这些函数必然会被resolve或reject调用，而resolve或reject函数里的内容已是异步执行，构造函数里的定义
    return (promise2 = new Promise(function (resolve, reject) {
      self.onResolvedCallback.push(function (value) {
        try {
          let x = onResolved(value);
          resolvePromise(promise2, x, resolve, reject);
        } catch (r) {
          reject(r);
        }
      });

      self.onRejectedCallback.push(function (reason) {
        try {
          let x = onRejected(reason);
          resolvePromise(promise2, x, resolve, reject);
        } catch (r) {
          reject(r);
        }
      });
    }));
  }
};

Promise.prototype.catch = function (onRejected) {
  return this.then(null, onRejected);
};

Promise.deferred = Promise.defer = function () {
  let dfd = {};
  dfd.promise = new Promise(function (resolve, reject) {
    dfd.resolve = resolve;
    dfd.reject = reject;
  });
  return dfd;
};

简单的发布订阅

class EventEmitter {
  constructor() {
    this._events = {};
  }

  //发送事件
  emit(eventName, data) {
    let returns = [];
    //data.eventName = eventName;
    if (Array.isArray(this._events[eventName])) {
      this._events[eventName].forEach((val, index) => {
        let returnValue = this._events[eventName][i](data);
        returns.push(returnValue);
      });
    }
    return returns;
  }
  on(eventName, callback, target) {
    this._events[eventName] = this._events[eventName] || [];
    this._events[eventName].push(callback.bind(target));
  }
  off(eventName, offCb) {
    if (this._events[eventName]) {
      let index = this._events[eventName].findIndex((cb) => cb === offCb);
      this._events[eventName].splice(index, 1);
      this._events[eventName] = [];
    }
  }
}

bind polyfill

if (!Function.prototype.bind) {
  Function.prototype.bind = function (oThis) {
    //oThis为需要绑定的对象也就是上例中的{a:20}
    // this为上例中的bFun，要求必须为函数类型
    if (typeof this !== "function") {
      // closest thing possible to the ECMAScript 5
      // internal IsCallable function
      throw new TypeError(
        "Function.prototype.bind - what is trying to be bound is not callable"
      );
    }
    //将bind函数传入的参数从第1个(index从0开始)开始转换成数组，因为第0个为传入的绑定对象。arguments为类数组
    let aArgs = Array.prototype.slice.call(arguments, 1),
      fToBind = this,
      fNOP = function () {},
      fBound = function () {
        // this instanceof fBound === true时,说明返回的fBound被当做new的构造函数调用
        // 由于使用new 方式创建的对象，this指向为对象的实例，此处判断如果使用new方式创建那么this应该为对象实例的this
        // 否则使用上下文绑定为传入的对象
        return fToBind.apply(
          this instanceof fBound ? this : oThis,
          // 获取调用时(fBound)的传参.bind 返回的函数入参往往是这么传递的
          // 函数的参数:应该为bind时传入的参数+调用生成的函数时传入的参数和
          aArgs.concat(Array.prototype.slice.call(arguments))
        );
      };

    // 维护原型关系
    if (this.prototype) {
      // Function.prototype doesn't have a prototype property
      fNOP.prototype = this.prototype;
    }
    // 下行的代码使fBound.prototype是fNOP的实例,因此
    // 返回的fBound若作为new的构造函数,new生成的新对象作为this传入fBound,新对象的__proto__就是fNOP的实例
    fBound.prototype = new fNOP();

    return fBound;
  };
}

实现一个图片的懒加载

代码参考自: 原生 JS 实现最简单的图片懒加载 (opens new window)

版本 1: 使用 getBoundingClientRect

function isInSight(el) {
  const bound = el.getBoundingClientRect();
  const clientHeight = window.innerHeight;
  //如果只考虑向下滚动加载
  return bound.top <= clientHeight + 100;
}

let index = 0;
function checkImgs() {
  const imgs = document.querySelectorAll(".my-photo");
  for (let i = index; i < imgs.length; i++) {
    if (isInSight(imgs[i])) {
      loadImg(imgs[i]);
      index = i;
    }
  }
}

function loadImg(el) {
  if (!el.src) {
    const source = el.dataset.src;
    el.src = source;
  }
}

function throttle(func, wait) {
  let timeout;
  return function () {
    let context = this;
    let args = arguments;
    if (!timeout) {
      timeout = setTimeout(() => {
        timeout = null;
        func.apply(context, args);
      }, wait);
    }
  };
}

// 调试

window.onload = checkImgs;
window.onscroll = throttle(checkImgs);

版本 2: 使用 IntersectionObserver

function checkImgs() {
  const imgs = Array.from(document.querySelectorAll(".my-photo"));
  imgs.forEach((item) => io.observe(item));
}

function loadImg(el) {
  if (!el.src) {
    const source = el.dataset.src;
    el.src = source;
  }
}

const io = new IntersectionObserver((ioes) => {
  ioes.forEach((ioe) => {
    const el = ioe.target;
    const intersectionRatio = ioe.intersectionRatio;
    if (intersectionRatio > 0 && intersectionRatio <= 1) {
      loadImg(el);
    }
    el.onload = el.onerror = () => io.unobserve(el);
  });
});

树的前序，中序，后序，层次遍历

参考自: JS 前序遍历、中序遍历、后序遍历、层序遍历详解，深度优先与广度优先区别，附 leetcode 例题题解答案 (opens new window)

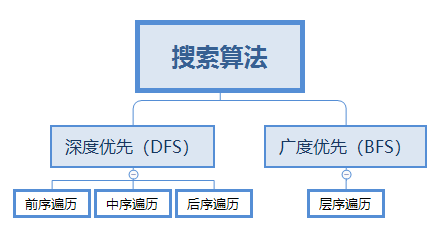
前序遍历

它满足根节点=>左子树=>右子树的顺序，

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
let preorderTraversal = function (root) {
  let res = [];
  // 遍历函数
  function traversal(root) {
    if (root !== null) {
      // 访问根节点的值
      res.push(root.val);
      if (root.left) {
        // 递归遍历左子树
        traversal(root.left);
      }
      if (root.right) {
        // 递归遍历右子树
        traversal(root.right);
      }
    }
  }
  traversal(root);
  return res;
};

中序遍历

中序遍历满足左子树=>根节点=>右子树的顺序进行查询

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
let inorderTraversal = function (root) {
  let res = [];
  // 遍历函数
  function traversal(root) {
    if (root !== null) {
      if (root.left) {
        // 递归遍历左子树
        traversal(root.left);
      }
      // 访问根节点的值
      res.push(root.val);
      if (root.right) {
        // 递归遍历右子树
        traversal(root.right);
      }
    }
  }
  traversal(root);
  return res;
};

后序遍历

左子树=>右子树=>根节点

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
let postorderTraversal = function (root) {
  let res = [];
  // 遍历函数
  function traversal(root) {
    if (root !== null) {
      if (root.left) {
        // 递归遍历左子树
        traversal(root.left);
      }
      if (root.right) {
        // 递归遍历右子树
        traversal(root.right);
      }
      // 访问根节点的值
      res.push(root.val);
    }
  }
  traversal(root);
  return res;
};

层序遍历

层序遍历满足从上到下，从左到右一层一层遍历的顺序

// 我们每遍历一层，都会将本层节点装到一个数组里，每往下推进一层，我们都得创建一个新的子数组
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
let levelOrder = function (root) {
  let res = [];

  function traversal(root, depth) {
    if (root !== null) {
      if (!res[depth]) {
        res[depth] = [];
      }
      res[depth].push(root.val);
      if (root.left) {
        traversal(root.left, depth + 1);
      }
      if (root.right) {
        traversal(root.right, depth + 1);
      }
    }
  }
  traversal(root, 0);
  return res;
};

实现数组的数据压缩

假设有如下数组:const testArr = [6, 8, 9, 7, 20, 30, 31, 32]; 我们期望相邻的自然数，需要结合在一起，并进行数据压缩。期望输出的值为[ [ 6, 9 ], [ 20 ], [ 30, 32 ] ]。

思路:

• 我们可以首先将数组从低到高排序，然后判断下一个数据是否和当前数据+1 相等
• 如果相等则 push 到同一个数组里面
• 最后只保留数组里的前后 2 个数据

const testArr = [6, 8, 9, 7, 20, 30, 31, 32];

function sortTest(arr) {
  // 从低到高
  let tempArr = arr.sort((a, b) => a - b);
  const result = [];
  let i = 0;
  let item = [];
  while (i < tempArr.length) {
    // 如果下一个数据和当前数据+1相等则直接push
    if (tempArr[i] + 1 == tempArr[i + 1]) {
      item.push(tempArr[i]);
    } else {
      // 否则吧最后一个数据push到数组里面，然后置空
      item.push(tempArr[i]);
      result.push(item);
      item = [];
    }
    i++;
  }
  let real = [];
  // 将[6,7,8]转换为[6,8]
  for (let each of result) {
    if (Array.isArray(each) && each.length > 2) {
      real.push([each[0], each[each.length - 1]]);
    } else {
      real.push(each);
    }
  }
  return real;
}
const start = Date.now();
console.log(sortTest(testArr));
console.log(Date.now() - start, "ms");

字符串压缩

给定一组字符，使用原地算法 (opens new window)将其压缩。

压缩后的长度必须始终小于或等于原数组长度。

数组的每个元素应该是长度为 1  的字符（不是 int 整数类型）。

在完成原地 (opens new window)修改输入数组后，返回数组的新长度。

进阶: 你能否仅使用 O(1) 空间解决问题？

示例 1:

输入: ["a","a","b","b","c","c","c"]

输出: 返回 6 ，输入数组的前 6 个字符应该是:["a","2","b","2","c","3"]

说明: "aa" 被 "a2" 替代。"bb" 被 "b2" 替代。"ccc" 被 "c3" 替代。

示例 2:

输入: ["a"]

输出: 返回 1 ，输入数组的前 1 个字符应该是:["a"]

解释: 没有任何字符串被替代。

示例 3:

输入: ["a","b","b","b","b","b","b","b","b","b","b","b","b"]

输出: 返回 4 ，输入数组的前 4 个字符应该是:["a","b","1","2"]。

解释: 由于字符 "a" 不重复，所以不会被压缩。"bbbbbbbbbbbb" 被 “b12” 替代。 注意每个数字在数组中都有它自己的位置。

let compress = function (chars) {
  let count = 1; //用来统计相同字符个数的变量
  for (let i = 0; i < chars.length; i++) {
    if (chars[i] === chars[i + 1]) {
      //前后项相同则count++，同时继续向后遍历
      count++;
    } else if (count !== 1) {
      // 替换数据，举个例子: [a,a,a,a,a,b]此时i=4,count=5，我们需要替换i=1到i=4的位置为'5'
      chars.splice(i - count + 2, count - 1, ...String(count));
      i = i - count + 2; // 替换完成之后，i需要更新位置为 i = 1
      count = 1;
    }
  }
  return chars.length;
};

冒泡排序

数组中有 n 个数，比较每相邻两个数，如果前者大于后者，就把两个数交换位置；这样一来，第一轮就可以选出一个最大的数放在最后面；那么经过 n-1（数组的 length - 1） 轮，就完成了所有数的排序。

时间复杂度： 平均时间复杂度 O(nn) 、最好情况 O(n)、最差情况 O(nn) 空间复杂度： O(1)

let arr = [3, 4, 1, 2];
function bubbleSort(arr) {
  let max = arr.length - 1;
  for (let j = 0; j < max; j++) {
    // 声明一个变量，作为标志位,如果某次循环完后，没有任何两数进行交换，就将标志位 设置为 true，表示排序完成，这样我们就可以减少不必要的排序，提高性能。

    let done = true;
    // 每一轮循环找到最大的放在最后，循环的次数为max-j
    for (let i = 0; i < max - j; i++) {
      if (arr[i] > arr[i + 1]) {
        let temp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = temp;
        done = false;
      }
    }
    if (done) {
      break;
    }
  }
  return arr;
}
bubbleSort(arr);

选择排序和插入排序

选择排序

function selectionSort(arr) {
  let len = arr.length;
  let minIndex, temp;
  for (let i = 0; i < len - 1; i++) {
    minIndex = i;
    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {
        // 寻找最小的数
        minIndex = j; // 将最小数的索引保存
      }
    }
    temp = arr[i];
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
  }
  return arr;
}

插入排序

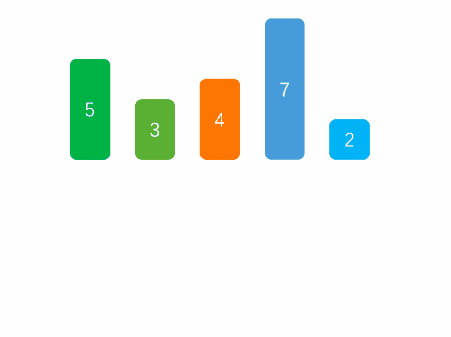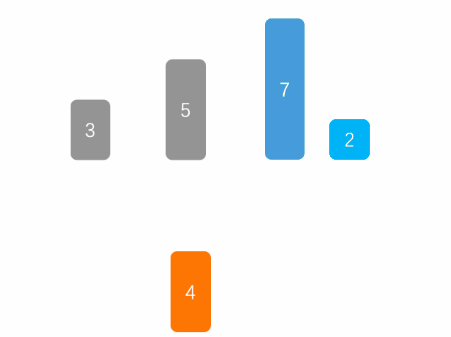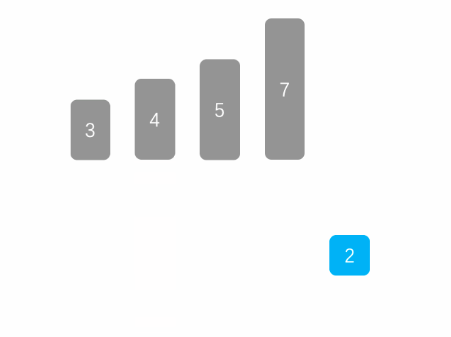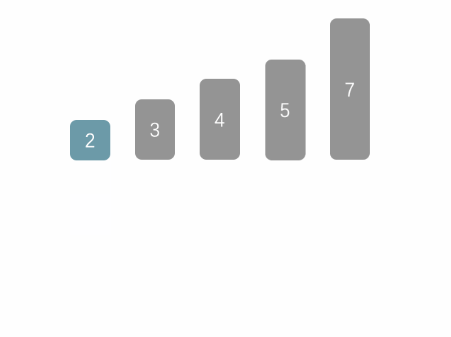
function insertionSort(arr) {
  var len = arr.length;
  var preIndex, current;
  for (var i = 1; i < len; i++) {
    preIndex = i - 1;
    current = arr[i];
    while (preIndex >= 0 && arr[preIndex] > current) {
      arr[preIndex + 1] = arr[preIndex];
      preIndex--;
    }
    arr[preIndex + 1] = current;
  }
  return arr;
}

快速排序【微信】

来源于:排序数组 (opens new window)

平均情况下快速排序的时间复杂度是 Θ(𝑛\lgn)，最坏情况是 Θ(𝑛2)。

快排的空间复杂度是 Θ(\lgn)，因为快排的实现是递归调用的， 而且每次函数调用中只使用了常数的空间，因此空间复杂度等于递归深度 Θ(\lgn)。

let sortArray = function (nums) {
  // 快速排序
  function quickSort(start, end, arr) {
    if (start < end) {
      let mid = sort(start, end, arr);
      // 注意，一定要是 start mid , mid+1 end 这种组合
      // 否则当首位最大的时候(mid返回0)，将会无限循环
      quickSort(start, mid, arr);
      quickSort(mid + 1, end, arr);
    }
    return arr;
  }

  function sort(start, end, arr) {
    // 取基准值
    let base = arr[start];

    let low = start;
    let high = end;

    while (low !== high) {
      // 从后往前，寻找比基准值小的值，赋给low位置(也就是取base值的位置)
      while (arr[high] >= base && high > low) {
        high--;
      }
      arr[low] = arr[high];
      // 从前往后，寻找比基准值大的值，赋给high位置
      while (arr[low] <= base && high > low) {
        low++;
      }
      arr[high] = arr[low];
    }
    arr[low] = base;
    return low;
  }
  return quickSort(0, nums.length - 1, nums);
};

堆排序

参考自:图解排序算法(三)之堆排序 (opens new window)

let len; // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量

function buildMaxHeap(arr) {
  // 建立大顶堆
  len = arr.length;
  // 从第一个非叶子结点开始
  for (let i = Math.floor(len / 2); i >= 0; i--) {
    heapify(arr, i);
  }
}

function heapify(arr, i) {
  // 堆调整
  let left = 2 * i + 1, // 非叶子节点的左子节点
    right = 2 * i + 2, // 非叶子节点的右子节点
    largest = i;

  if (left < len && arr[left] > arr[largest]) {
    largest = left;
  }

  if (right < len && arr[right] > arr[largest]) {
    largest = right;
  }

  if (largest != i) {
    // 如果存在交换，则需要一直交换
    swap(arr, i, largest);
    heapify(arr, largest);
  }
}

function swap(arr, i, j) {
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

function heapSort(arr) {
  // 构建大顶堆
  buildMaxHeap(arr);
  // 排序，每一次for循环找出一个当前最大值，数组长度减一
  for (let i = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i); // 根节点与最后一个节点交换
    len--;
    heapify(arr, 0);
  }
  return arr;
}

let arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];

console.log(heapSort(arr));

是否为有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']'  的字符串 s ，判断字符串是否有效。

有效字符串需满足:

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。

示例 1:

**输入:**s = "()" **输出:**true

示例  2:

**输入:**s = "()[]{}" **输出:**true

示例  3:

**输入:**s = "(]" **输出:**false

示例  4:

**输入:**s = "([)]" **输出:**false

示例  5:

**输入:**s = "{[]}" **输出:**true

let isValid = function (s) {
  // 1.判断数组是否为 空 或 奇数，若有，则跳出直接输出 false。
  const length = s.length;
  if (!s || length % 2 === 1) {
    return false;
  }
  // 2.遍历数组，若遇到 左括号，入栈（push）。遇到右括号，则先与栈顶匹配，若类型匹配，则出栈。若不匹配，直接 false。
  const stack = [];
  for (let i = 0; i < length; i += 1) {
    const c = s[i];
    if (c === "(" || c === "{" || c === "[") {
      stack.push(c);
    } else {
      const t = stack[stack.length - 1];
      if (
        (t === "(" && c === ")") ||
        (t === "{" && c === "}") ||
        (t === "[" && c === "]")
      ) {
        stack.pop();
      } else {
        return false;
      }
    }
  }
  // 3.判断 栈是否已空。
  return stack.length === 0 ? true : false;
};

是否为有效括号（带*号）

给定一个只包含三种字符的字符串：（ ，）  和 *，写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则：

任何左括号 (  必须有相应的右括号 )。 任何右括号 )  必须有相应的左括号 ( 。 左括号 ( 必须在对应的右括号之前 )。 *  可以被视为单个右括号 ) ，或单个左括号 ( ，或一个空字符串。 一个空字符串也被视为有效字符串。 示例 1:

输入: "()" 输出: True 示例 2:

输入: "(*)" 输出: True 示例 3:

输入: "(*))" 输出: True

var checkValidString = function (s) {
  const leftStack = [];
  const asteriskStack = [];
  const n = s.length;
  for (let i = 0; i < n; i++) {
    const c = s[i];
    if (c === "(") {
      leftStack.push(i);
    } else if (c === "*") {
      asteriskStack.push(i);
    } else {
      if (leftStack.length) {
        leftStack.pop();
      } else if (asteriskStack.length) {
        asteriskStack.pop();
      } else {
        return false;
      }
    }
  }
  while (leftStack.length && asteriskStack.length) {
    const leftIndex = leftStack.pop();
    const asteriskIndex = asteriskStack.pop();
    // 如果(的数量比*数量多，则一定会为false
    if (leftIndex > asteriskIndex) {
      return false;
    }
  }
  // 遍历完成，可能(比较多那么就为false，也有可能通过while循环之后*比较多，(没有了，*就可以替代为任意数，可以返回为true
  return leftStack.length === 0;
};

二分查找求平方根

给你一个非负整数 x ，计算并返回  x  的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4 输出：2 示例 2：

输入：x = 8 输出：2 解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

方法 1:二分法 思路：从 0-x 不断二分，直到 复杂度分析：时间复杂度 O(logx)，即为二分查找需要的次数。空间复杂度 O(1) js:

var mySqrt = function (x) {
  let left = 0;
  let right = x;
  while (left <= right) {
    let mid = left + ((right - left) >> 1); //中间位置索引 x>>1 表示除以2并取整，缩小一下遍历的范围
    if (mid * mid <= x) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  return right;
};

TIP

作者：chen-wei-f 链接：https://leetcode-cn.com/problems/sqrtx/solution/er-fen-fa-dai-ma-jian-ji-by-chen-wei-f-52iw/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1:

**输入:**l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]

示例 2:

**输入:**l1 = [], l2 = [] 输出:[]

示例 3:

**输入:**l1 = [], l2 = [0] 输出:[0]

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
let mergeTwoLists = function (l1, l2) {
  const prehead = new ListNode(-1);

  let prev = prehead;
  while (l1 != null && l2 != null) {
    if (l1.val <= l2.val) {
      prev.next = l1;
      l1 = l1.next;
    } else {
      prev.next = l2;
      l2 = l2.next;
    }
    prev = prev.next;
  }

  // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
  prev.next = l1 === null ? l2 : l1;

  return prehead.next;
};

实现两个树的 diff

//要找到两个二叉树之间有什么不同
//1.新增了节点
//2.删除了节点
//3.修改了节点
//不同的地方，存入diffList中
function diffTree(root1, root2, diffList) {
  let diff = diffList || [];
  if (root1 == root2) return diff; //若两者是同一颗树，则直接返回diff
  if (root1 == null && root2 != null) {
    //root2新增了一个节点
    diff.push({
      type: "新增",
      origin: null,
      new: root2,
    });
  } else if (root1 != null && root2 == null) {
    //root2删除了一个节点
    diff.push({
      type: "删除",
      origin: root1,
      new: null,
    });
  } else if (root1.value != root2.value) {
    //root2节点的值被修改了
    diff.push({
      type: "修改",
      origin: root1.value,
      new: root2.value,
    });
    //二叉树的节点值被修改，还需要再次判断子节点
    diffTree(root1.left, root2.left, diff); //判断左子树
    diffTree(root1.right, root2.right, diff); //判断右子树
  } else {
    diffTree(root1.left, root2.left, diff); //判断左子树
    diffTree(root1.right, root2.right, diff); //判断右子树
  }
  return diff;
}
let diffList = [];
let diff = diffTree(nodeA, a, diffList);
console.log(diff);

爬楼梯

假设你正在爬楼梯。需要 n  阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

**注意:**给定 n 是一个正整数。

示例 1:

输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2:

输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

题解

我们用 f(x) 表示爬到第 x 级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，所以我们可以列出如下式子:

f(x)=f(x−1)+f(x−2)

它意味着爬到第 x 级台阶的方案数是爬到第 x - 1 级台阶的方案数和爬到第 x - 2 级台阶的方案数的和。很好理解，因为每次只能爬 1 级或 2 级，所以 f(x) 只能从 f(x−1) 和 f(x - 2) 转移过来，而这里要统计方案总数，我们就需要对这两项的贡献求和。

代码参考自:leetcode (opens new window)

let climbStairs = function (n) {
  // f(0)=1；从第 0 级到第 1 级也只有一种方案，即爬一级，f(1) = 1
  // p 为 x-2 ,q为x-1,r为结果
  let p = 0,
    q = 0,
    r = 1;
  for (let i = 1; i <= n; ++i) {
    p = q;
    q = r;
    r = p + q;
  }
  return r;
};


// 算法2

let climbStairs = function (n) {
  if (n <= 2) {
    return n;
  }
  return climbStairs(n - 1) + climbStairs(n - 2);
};
console.log(climbStairs(10));

事件循环测试

Macrotask 常见的任务：

• setTimeout ,优先级优先于 setImmediate
• setInterval
• setImmediate
• I/O
• 用户交互操作，UI 渲染

Microtask 常见的任务：

• Promise(重点)

• process.nextTick(nodejs) , 优先级优先于 Promise

• Object.observe(不推荐使用)

• requestAnimationFrame: 不属于微任务也不属于宏任务，是属于任务。是一个在重绘之前执行的一个操作，而重绘操作一般是宏任务之前、微任务之后执行

特性：

1. 当开始执行它的回调时，在此刻之前注册的所有该类回调，会一次性执行完(一个 loop 内，这点很关键)
2. 如果以自身递归调用的方式(raf 回调内递归调用 raf，使用该 api 的正确姿势)，它的触发时机总是与浏览器的渲染频率保持一致。

测试

console.log("Script开始");
setTimeout(() => {
  console.log("宏任务1（setTimeout)");
  Promise.resolve().then(() => {
    console.log("微任务promise2");
  });
}, 0);
setImmediate(() => {
  console.log("宏任务2");
});
setTimeout(() => {
  console.log("宏任务3（setTimeout)");
}, 0);
console.log("Script结束");
Promise.resolve().then(() => {
  console.log("微任务promise1");
});
process.nextTick(() => {
  console.log("微任务nextTick");
});

// node 11.x 以后
// Script开始
// Script结束
// 微任务nextTick
// 微任务promise1
// 宏任务1（setTimeout)
// 微任务promise2
// 宏任务3（setTimeout)
// 宏任务2（setImmediate)

测试 1

console.log(1);
setTimeout(function () {
  //settimeout1
  console.log(2);
}, 0);
const intervalId = setInterval(function () {
  //setinterval1
  console.log(3);
}, 0);
setTimeout(function () {
  //settimeout2
  console.log(10);
  new Promise(function (resolve) {
    //promise1
    console.log(11);
    resolve();
  })
    .then(function () {
      console.log(12);
    })
    .then(function () {
      console.log(13);
      clearInterval(intervalId);
    });
}, 0);

requestAnimationFrame(() => {
  console.log("raf1");
});

//promise2
Promise.resolve()
  .then(function () {
    console.log(7);
  })
  .then(function () {
    console.log(8);
  });
console.log(9);
requestAnimationFrame(() => {
  console.log("raf2");
});

输出的结果如下:

1
9
7
8
raf1
raf2
2
3
10
11
12
13

async 测试

async function async1() {
  console.log("async1 start");
  Promise.resolve(async2()).then(() => console.log("async1 end"));
}
async function async2() {
  console.log("async2");
}
async1();
new Promise(function (resolve) {
  console.log("promise1");
  resolve();
}).then(function () {
  console.log("promise2");
});
console.log("script end");

输出的结果如下:

async1 start
async2
promise1
script end
sync1 end
promise2

LRU(最近最少使用缓存)

题目

请你设计并实现一个满足   LRU (最近最少使用) 缓存 (opens new window) 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量  capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value)  如果关键字  key 已经存在，则变更其数据值  value ；如果不存在，则向缓存中插入该组  key-value 。如果插入操作导致关键字数量超过  capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入 ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"] [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]] 输出 [null, null, null, 1, null, -1, null, -1, 3, 4]

解释

LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4

理解题意

• 数据被读取了，就是被使用了，所在的位置要刷新，浮到“顶部”。
• 写入数据时：
  • 之前就存在的：更新数据，刷新位置。
  • 之前不存在的：有位置就直接写入，没有位置，就删掉最久没有使用的条目，再写入。
• 要求 get 和 put 为 O ( 1 ) O(1) O(1)，这俩操作都可能导致条目的移动(有删除操作)，所以删除操作也要是 O ( 1 ) O(1) O(1)。

选择什么数据结构？

• O ( 1 ) O(1) O(1) 的快速查找，就哈希表了。
• 光靠哈希表可以吗？
  • 哈希表是无序的，无法知道里面的键值对哪些最近访问过，哪些很久没访问。
• 快速删除，谁合适？
  • 数组？元素的插入/移动/删除都是 O ( n ) O(n) O(n)。不行。
  • 单向链表？删除节点需要访问前驱节点，只能花 O ( n ) O(n) O(n) 从前遍历查找。不行。
  • 双向链表，结点有前驱指针，删除/移动节点都是纯纯的指针变动，都是 O ( 1 ) O(1) O(1)。

双向链表、哈希表，各自的角色

• 双向链表的结点：存 key 和 对应的数据值。
• 哈希表的存在意义：快速访问【存储于双向链表】的数据，不是它自己存数据
  • key：双向链表中存的 key
  • value：链表结点的引用。

定义 ListNode 节点

class ListNode {
  constructor(key, value) {
    this.key = key;
    this.value = value;
    this.next = null;
    this.prev = null;
  }
}

定义 LRUCache

class LRUCache {
  constructor(capacity) {
    this.capacity = capacity; // 容量
    this.hash = {}; // 哈希表
    this.count = 0; // 缓存数目
    this.dummyHead = new ListNode(); // 虚拟头结点
    this.dummyTail = new ListNode(); // 虚拟尾节点
    this.dummyHead.next = this.dummyTail;
    this.dummyTail.prev = this.dummyHead; // 还未添加真实节点，将虚拟头尾节点相连
  }
}

设计 dummyHead 和 dummyTail 的意义

• 虚拟头尾节点，只是为了让对真实头尾节点的操作，和对其他节点的操作一致，方便快速访问头尾节点。

(opens new window)get 方法实现

• 哈希表中找不到对应的值，则返回 -1。被读取的节点，要刷新它的位置，移动到链表头部

get(key) {
  let node = this.hash[key]      // 从哈希表中，获取对应的节点
  if (node == null) return -1    // 如果节点不存在，返回-1
  this.moveToHead(node)          // 被读取了，该节点移动到链表头部
  return node.value              // 返回出节点值
}

• moveToHead方法实现

  moveToHead(node) {
    this.removeFromList(node) // 先从链表中删除
    this.addToHead(node)      // 再加到链表的头部
  }
  removeFromList(node) {
    let temp1 = node.prev     // 暂存它的后继节点
    let temp2 = node.next     // 暂存它的前驱节点
    temp1.next = temp2        // 前驱节点的next指向后继节点
    temp2.prev = temp1        // 后继节点的prev指向前驱节点
  }
  addToHead(node) {                 // 插入到虚拟头结点和真实头结点之间
    node.prev = this.dummyHead      // node的prev指针，指向虚拟头结点
    node.next = this.dummyHead.next // node的next指针，指向原来的真实头结点
    this.dummyHead.next.prev = node // 原来的真实头结点的prev，指向node
    this.dummyHead.next = node      // 虚拟头结点的next，指向node
  }
  

put 方法实现

• 写入新数据，要先检查容量，看看是否要删“老家伙”，然后创建新的节点，添加到链表头部(最不优先被淘汰)，哈希表也更新一下。
• 写入已有的数据，则更新数据值，刷新节点的位置。

put(key, value) {
  let node = this.hash[key]            // 获取链表中的node
  if (node == null) {                  // 不存在于链表，是新数据
    if (this.count == this.capacity) { // 容量已满
      this.removeLRUItem()             // 删除最远一次使用的数据
    }
    let newNode = new ListNode(key, value) // 创建新的节点
    this.hash[key] = newNode          // 存入哈希表
    this.addToHead(newNode)           // 将节点添加到链表头部
    this.count++                      // 缓存数目+1
  } else {                   // 已经存在于链表，老数据
    node.value = value       // 更新value
    this.moveToHead(node)    // 将节点移到链表头部
  }
}

• removeLRUItem 方法实现

    removeLRUItem() {               // 删除“老家伙”
      let tail = this.popTail()     // 将它从链表尾部删除
      delete this.hash[tail.key]    // 哈希表中也将它删除
      this.count--                  // 缓存数目-1
    }
    popTail() {                      // 删除链表尾节点
      let tail = this.dummyTail.prev // 通过虚拟尾节点找到它
      this.removeFromList(tail)      // 删除该真实尾节点
      return tail                    // 返回被删除的节点
    }

整体代码

class ListNode {
  constructor(key, value) {
    this.key = key;
    this.value = value;
    this.next = null;
    this.prev = null;
  }
}

class LRUCache {
  constructor(capacity) {
    this.capacity = capacity;
    this.hash = {};
    this.count = 0;
    this.dummyHead = new ListNode();
    this.dummyTail = new ListNode();
    this.dummyHead.next = this.dummyTail;
    this.dummyTail.prev = this.dummyHead;
  }

  get(key) {
    let node = this.hash[key];
    if (node == null) return -1;
    this.moveToHead(node);
    return node.value;
  }

  put(key, value) {
    let node = this.hash[key];
    if (node == null) {
      if (this.count == this.capacity) {
        this.removeLRUItem();
      }
      let newNode = new ListNode(key, value);
      this.hash[key] = newNode;
      this.addToHead(newNode);
      this.count++;
    } else {
      node.value = value;
      this.moveToHead(node);
    }
  }

  moveToHead(node) {
    this.removeFromList(node);
    this.addToHead(node);
  }

  removeFromList(node) {
    let temp1 = node.prev;
    let temp2 = node.next;
    temp1.next = temp2;
    temp2.prev = temp1;
  }

  addToHead(node) {
    // 注意这里是有先后顺序的，优先设置当前node，且需要先设置pre,然后next
    node.prev = this.dummyHead;
    node.next = this.dummyHead.next;
    this.dummyHead.next.prev = node;
    this.dummyHead.next = node;
  }

  removeLRUItem() {
    let tail = this.popTail();
    delete this.hash[tail.key];
    this.count--;
  }

  popTail() {
    let tail = this.dummyTail.prev;
    this.removeFromList(tail);
    return tail;
  }
}

两个有序数组合并

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

示例 1：

输入：1->2->4, 1->3->4 输出：1->1->2->3->4->4 限制：

0 <= 链表长度 <= 1000

function ListNode(val) {
  this.val = val;
  this.next = null;
}
const mergeTwoLists = (l1, l2) => {
  // 定义一个虚拟节点，最后返回虚拟节点的下一个节点
  const res = new ListNode(0);
  // 定义p指向虚拟节点
  let p = res;
  // 定义p1,p2分别指向两个链表头部
  let [p1, p2] = [l1, l2];
  // 当p1, p2都有值的时候
  while (p1 && p2) {
    // 如果p1指向的值小，则p指向p1的值
    // p1右移
    // 否则p指向p2的值，p2右移
    if (p1.val < p2.val) {
      p.next = p1;
      p1 = p1.next;
    } else {
      p.next = p2;
      p2 = p2.next;
    }
    // 记得p也要右移
    p = p.next;
  }
  // 到最后退出循环了，p1,p2肯定有且只有一个是null
  // 那么另一个不是null的还没有连接到p上
  // 把p再连接到不是null的那个
  p.next = p1 ? p1 : p2;
  // 返回虚拟节点的下一个节点
  return res.next;
};

TIP

作者：lzxjack 链接：https://leetcode-cn.com/problems/he-bing-liang-ge-pai-xu-de-lian-biao-lcof/solution/bian-bian-li-bian-he-bing-by-jack_lzx-mwa3/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

实现一个 trim 函数

String.prototype.trim = function () {
  return this.replace(/^\s+|\s+$/g, "");
};

扁平数据结构转Tree

解法1：不考虑性能实现，递归遍历查找

/**
 * 递归查找，获取children
 */
const getChildren = (data, result, pid) => {
  for (const item of data) {
    if (item.pid === pid) {
      const newItem = {...item, children: []};
      result.push(newItem);
      getChildren(data, newItem.children, item.id);
    }
  }
}

/**
* 转换方法
*/
const arrayToTree = (data, pid) => {
  const result = [];
  getChildren(data, result, pid)
  return result;
}

解法2：不用递归，也能搞定

主要思路是先把数据转成Map去存储，之后遍历的同时借助对象的引用，直接从Map找对应的数据做存储

function arrayToTree(items) {
  const result = [];   // 存放结果集
  const itemMap = {};  // 
    
  // 先转成map存储
  for (const item of items) {
    itemMap[item.id] = {...item, children: []}
  }
  
  for (const item of items) {
    const id = item.id;
    const pid = item.pid;
    const treeItem =  itemMap[id];
    if (pid === 0) {
      result.push(treeItem);
    } else {
      if (!itemMap[pid]) {
        itemMap[pid] = {
          children: [],
        }
      }
      itemMap[pid].children.push(treeItem)
    }

  }
  return result;
}

从上面的代码我们分析，有两次循环，该实现的时间复杂度为O(2n)，需要一个Map把数据存储起来，空间复杂度O(n)

解法3: 最优性能

function arrayToTree(items) {
  const result = [];   // 存放结果集
  const itemMap = {};  // 
  for (const item of items) {
    const id = item.id;
    const pid = item.pid;

    if (!itemMap[id]) {
      itemMap[id] = {
        children: [],
      }
    }

    itemMap[id] = {
      ...item,
      children: itemMap[id]['children']
    }

    const treeItem =  itemMap[id];

    if (pid === 0) {
      result.push(treeItem);
    } else {
      if (!itemMap[pid]) {
        itemMap[pid] = {
          children: [],
        }
      }
      itemMap[pid].children.push(treeItem)
    }

  }
  return result;
}